Ahli-Ahli Matematika Wanita yang Terkenal

Jika kita mengamati kembali sejarah Matematika, ternyata bidang Matematika tidak lepas dari pengaruh beberapa Wanita yang luar biasa. Mereka sungguh menekuni Matematika, sains, dan filosofi. Berikut adalah beberapa sumbangan dari "Para Wanita Jenius" yang membuat mereka terkenal dalam bidang intelektual ini.

1. Hypatia

Hypatia adalah ahli Matematika pertama yang diakui. Dia lahir di Alexandria, Mesir, sekitar tahun 350 dan ia merupakan seorang sarjana yang diakui. Selain menjadi ahli matematika, ia juga adalah seorang ahli astronomi dan filsafat. Ia juga percaya pada teori yang dikemukakan oleh Plato dan Aristoteles. Ia meninggal dunia akibat dari kemarahan massa Kristen pada waktu itu. Namun masih banyak kebingungan dan perdebatan, apakah ia meninggal pada tahun 370 atau tahun 415 setelah masehi. Kontribusinya yang kekal dalam dunia matematika tidak habis-habisnya digunakan untuk penelitian di berbagai topik. Pekerjaan utamanya adalah sebagai berikut:
a) Ia menulis suatu komentar pada volume ke-13 dari buku teks Matematika Yunani yang terkenal yaitu "Artihmetica".
b) Dia mengubah Ptolemy dari versi terkenalnya "Almagest".
c) Dia mengubah komentar ayahnya pada "Euclid's Elements" atau "Elemen Euclid".
d) Ia juga membuat komentar pada sebuah pekerjaan terkenal yaitu Conics yang dibuat oleh "Apollonius".


2. Maria Gaetana Agnesi

Ia adalah seorang anak yang berbakat, seorang ahli bahasa Italia dan matematika. Maria adalah seorang wanita yang memiliki multi talenta. Ia Lahir dari sebuah keluarga yang kaya pada tahun 1718 dan dia adalah anak ke 21 dari orang tuanya. Ia juga menguasai lebih dari separuh lusin bahasa. Ia adalah tokoh yang sangat terkenal di bidang matematika. Kontribusinya adalah sebagai berikut:
a) Ia menulis buku pertama yang memperkenalkan Integral dan Kalkulus Diferensial.
b) Ia menulis "Instituzioni analitiche ad uso della gioventu italiana"; sebuah master piece yang dianggap sebagai perluasan yang terbaik untuk karya Euler.
c) Ia juga menulis sebuah perjanjian yang tidak bisa diterbitkan, namun karya itu sangat dihargai dan dipuja-puja banyak orang.
d) Ia menentukan persamaan dari suatu kurva yang aneh, yang kemudian dikenal sebagai "Witch dari Agnesi".


3. Sophie Germain

Sophie lahir dari sebuah keluarga kaya kelas atas di Perancis, pada tahun 1776, di mana tahun ini merupakan masa Revolusi bagi rakyat Amerika. Apapun "Pekerjaan Otak" yang dilakukan wanita pada zaman itu dianggap sebagai pekerjaan yang tidak sehat dan berbahaya bagi wanita. Karena hal inilah, Sophie selalu menghadapi banyak masalah dalam mendapatkan pendidikan, karena adanya aturan yang tabu tersebut di masyarakat. Meskipun demikian, ia tetap belajar matematika dan mengukir cita-citanya dalam bidang ini. Dia sering disebut sebagai "The Revolutionary Mathematician". Kontribusinya adalah sebagai berikut:
a) Pada awalnya, ia bekerja pada Teori Bilangan dan memberikan banyak yang Teorema menarik pada bilangan prima. Ia bahkan menemukan identitas baru, sehingga banyak bilangan seperti itu yang saat ini disebut sebagai "Sophie Germain primes" atau "Bilangan Prima Sophie Germain".
b) Karyanya tentang "Fermat's Last theorem" merupakan suatu jalan pintas yang menarik.
c) Dia adalah wanita pertama yang menghadiri "Academie des Science" dan "Institut de France' session".


4. Ada Lovelace

Ada Lovelace adalah anak perempuan dari seorang penyair terkenal, "Lord Byron". Ia lahir pada tanggal 10 Desember 1815 di Inggris dan ia dinobatkan sebagai "Programmer Pertama" di dunia. Dialah yang meletakkan dasar untuk dunia software dan komputer. Pada tahun 1980, muncullah bahasa pemrograman komputer "Ada". Kontribusinya adalah sebagai berikut:
Dia diakui satu-satunya yang telah menulis simbol dan kode sesuai dengan aturan, untuk komputer mekanik awal milik Charles Babbage, yaitu "The Analytical Engine".


5. Sofia Kovalevskaya

Ia lahir pada 15 Januari 1850 di Moskow, Rusia. Dia adalah ahli Matematika wanita pertama dan utama di Rusia. Ia berani menentang kakek-neneknya demi melanjutkan studi yang lebih tinggi. Dia dikenal dengan karya-karyanya sebagai berikut:
a) Dia melakukan penelitian pada persamaan diferensial yang dikenal sebagai "Kovalevskaya Top".
b) Ia bekerja mengembangkan "Teorema Cauchy-Kovalevskaya", sebuah teorema yang sangat dasar untuk membantu memahami persamaan diferensial.


6. Amalie Emmy Noether

Ia lahir pada 23 Maret 1882 di Jerman. Amalie adalah seorang ahli matematika revolusioner mampu bekerja di berbagai bidang. Albert Einstein mengatakan bahwa dia adalah "Wanita yang paling penting dalam sejarah matematika, karena pendidikan tingginya". Karya-karyanya antara lain:
a) Penelitian lengkap mengenai Aljabar Abstrak dan Teori Fisika.
b) Teori Path-breaking dalam bidang aljabar.
c) Salah satu teorema terkenal dari ilmu fisika yaitu "Teorema Noether", menghubungkan konservasi hukum, dan simetri yang diusulkan oleh Noether.

Fakta-Fakta Menarik Mengenai Phi

Ada bukti-bukti sejarah untuk membuktikan bahwa luas dari sebuah lingkaran dihitung dengan rumus "3 kali kuadrat dari radius" menurut orang Babylonia. Sebuah tablet Babylonia kuno yang ditemukan antara 1900 - 1680 SM memiliki nilai phi sebagai 3,125.

Bangsa Mesir kuno menghitung luas sebuah lingkaran menggunakan rumus [(8D)/9]², di mana "D" adalah diameter lingkaran. Rumus ini memberikan sebuah perkiraan bahwa nilai pi adalah 3,1605.

Seorang ahli matematika kuno Archimedes dari Syracuse yang hidup antara 287 - 212 SM mengambil nilai phi berdasarkan luas dari poligon biasa yang berada di dalam lingkaran dan luas dari sebuah poligon biasa tersebut dibatasi oleh lingkaran.

Fakta-Fakta Menarik Mengenai Phi ()
(saya mohon maaf, sebenarnya posisi penulisan Phi bukan ke atas, ini dikarenakan galat dari hosting image)

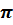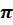Pada tahun 1706, seorang ahli Matematika bahasa Inggris memperkenalkan abjad Yunani phi () untuk mewakili nilai yang dikatakan. Namun, pada tahun 1737, Euler resmi mengadopsi simbol ini untuk mewakili bilangan.

Pada tahun 1897, legislatif dari Indiana mencoba menentukan nilai yang paling akurat untuk phi. Namun ternyata kebijakan ini tidak berhasil.

Sebagian besar orang pada waktu itu tidak mengetahui fakta bahwa lingkaran memiliki jumlah sudut yang tak terbatas. Nilai dari phi adalah banyaknya diameter lingkaran yang akan dipaskan dengan keliling lingkaran.

Nilai dari phi adalah 22 / 7 dan ditulis sebagai = 22 / 7 atau = 3,14.

Nilai phi dengan 100 tempat desimal pertama adalah: 3,141592653589793238462643383279502884197169399375105820974944
5923078164062862089986280348253421170679

Fakta menarik lainnya adalah Anda tidak akan menemukan nol dalam 31 digit pertama dalam dari phi.

Di samping perhitungan geometri sehari-hari, nilai phi juga digunakan dalam berbagai persamaan ilmiah termasuk rekayasa genetika, mengukur reaksi, distribusi normal, dan sebagainya.

Tahukah Anda bahwa phi tidak hanya sebuah nomor irasional tetapi juga bilangan yang sulit dipahami?
Fakta menarik lainnya tentang phi diambil dari huruf Yunani "Piwas". Itu juga merupakan Abjad Yunani yang ke-16.

Seorang pengusaha di Cleveland, AS, menerbitkan buku pada pada tahun 1931 untuk mengumumkan bahwa nilai pi adalah 256/81.
Jika Anda mencetak miliaran dari desimal phi, maka angka itu akan merentang dari New York City ke Kansas.


Fakta-Fakta Menarik Lainnya Lagi Mengenai Phi

Tahukah Anda Yasumasa Kanada, seorang profesor di Universitas Tokyo?? Ia membutukan waktu sekitar 116 jam untuk menemukan sebanyak 6442450000 tempat desimal Phi dengan komputer.

Pada tahun 1706, John Machin memperkenalkan suatu rumus untuk menghitung nilai phi, yaitu :
/ 4 = 4 * arc tan (1 / 5) - arc tan (1 / 239).

Pada tahun 1949, ia juga menghabiskan waktu sekitar 70 jam untuk menghitung 2.037 tempat desimal phi menggunakan ENIAC (Electronic Numeric Integrator and Computer).

Seorang Ahli Matematika Jerman, Ludolph van Ceulen, mendedikasikan seluruh hidupnya untuk menghitung 35 tempat desimal pertama phi.

Pada tahun 1768, Johann Lambert membuktikan nilai Phi adalah sebuah bilangan irasional, dan pada tahun 1882, Ferdinand Lindemann yang juga Ahli matematika terkenal membuktikan Phi adalah bilangan yang sulit dipahami.

Ada orang yang hafal semua angka desimal phi. Orang tersebut membuat lagu dan musik berdasarkan digit dari phi. Dalam kehidupan ini, memang terdapat banyak fakta yang menarik dan menyenangkan mengenai phi.

Misteri Bilangan Lubang Hitam : 123

Dalam astronomi dan fisika, kita mengenal adanya suatu fenomena alam yang sangat menarik yaitu lubang hitam (black hole). Lubang hitam adalah suatu entitas yang memiliki medan gravitasi yang sangat kuat sehingga setiap benda yang telah jatuh di wilayah horizon peristiwa (daerah di sekitar inti lubang hitam), tidak akan bisa kabur lagi. Bahkan radiasi elektromagnetik seperti cahaya pun tidak dapat melarikan diri, akibatnya lubang hitam menjadi "tidak kelihatan".

Ternyata, dalam matematika juga ada fenomena unik yang mirip dengan fenomena lubang hitam yaitu bilangan lubang hitam. Bagaimana sebenarnya bilangan lubang hitam itu? Mari kita bermain-main sebentar dengan angka.

Coba pilih sesuka hati Anda sebuah bilangan asli (bilangan mulai dari 1 sampai tak hingga). Sebagai contoh, katakanlah 141.985. Kemudian hitunglah jumlah digit genap, digit ganjil, dan total digit bilangan tersebut. Dalam kasus ini, kita dapatkan 2 (dua buah digit genap), 4 (empat buah digit ganjil), dan 6 (enam adalah jumlah total digit). Lalu gunakan digit-digit ini (2, 4, dan 6) untuk membentuk bilangan berikutnya, yaitu 246.

Ulangi hitung jumlah digit genap, digit ganjil, dan total digit pada bilangan 246 ini. Kita dapatkan 3 (digit genap), 0 (digit ganjil), dan 3 (jumlah total digit), sehingga kita peroleh 303. Ulangi lagi hitung jumlah digit genap, ganjil, dan total digit pada bilangan 303. (Catatan: 0 adalah bilangan genap). Kita dapatkan 1, 2, 3 yang dapat dituliskan 123.

Jika kita mengulangi langkah di atas terhadap bilangan 123, kita akan dapatkan 123 lagi. Dengan demikian, bilangan 123 melalui proses ini adalah lubang hitam bagi seluruh bilangan lainnya. Semua bilangan di alam semesta akan ditarik menjadi bilangan 123 melalui proses ini, tak satu pun yang akan lolos.

Tapi benarkah semua bilangan akan menjadi 123? Sekarang mari kita coba suatu bilangan yang bernilai sangat besar, sebagai contoh katakanlah 122333444455555666666777777788888888999999999. Jumlah digit genap, ganjil, dan total adalah 20, 25, dan 45. Jadi, bilangan berikutnya adalah 202.545. Lakukan lagi iterasi (pengulangan), kita peroleh 4, 2, dan 6; jadi sekarang kita peroleh 426. Iterasi sekali lagi terhadap 426 akan menghasilkan 303 dan iterasi terakhir dari 303 akan diperoleh 123. Sampai pada titik ini, iterasi berapa kali pun terhadap 123 akan tetap diperoleh 123 lagi. Dengan demikian, 123 adalah titik absolut sang lubang hitam dalam dunia bilangan.

Namun, apakah mungkin saja ada suatu bilangan, terselip di antara rimba raya alam semesta bilangan yang jumlahnya tak terhingga ini, yang dapat lolos dari jeratan maut sang bilangan lubang hitam, sang 123 yang misterius ini?

Sumber: http://www.forumsains.com/artikel/misteri-bilangan-lubang-hitam-123/?PHPSESSID=37b5sf8mpb9ocq8pmfpac7bau4

Misteri Bilangan Nol

Ratusan tahun yang lalu, manusia hanya mengenal 9 lambang bilangan yakni 1, 2, 2, 3, 5, 6, 7, 8, dan 9. Kemudian, datang angka 0, sehingga jumlah lambang bilangan menjadi 10 buah. Tidak diketahui siapa pencipta bilangan 0, bukti sejarah hanya memperlihatkan bahwa bilangan 0 ditemukan pertama kali dalam zaman Mesir kuno. Waktu itu bilangan nol hanya sebagai lambang. Dalam zaman modern, angka nol digunakan tidak saja sebagai lambang, tetapi juga sebagai bilangan yang turut serta dalam operasi matematika. Kini, penggunaan bilangan nol telah menyusup jauh ke dalam sendi kehidupan manusia. Sistem berhitung tidak mungkin lagi mengabaikan kehadiran bilangan nol, sekalipun bilangan nol itu membuat kekacauan logika. Mari kita lihat.

Nol, penyebab komputer macet

Pelajaran tentang bilangan nol, dari sejak zaman dahulu sampai sekarang selalu menimbulkan kebingungan bagi para pelajar dan mahasiswa, bahkan masyarakat pengguna. Mengapa? Bukankah bilangan nol itu mewakili sesuatu yang tidak ada dan yang tidak ada itu ada, yakni nol. Siapa yang tidak bingung? Tiap kali bilangan nol muncul dalam pelajaran Matematika selalu ada ide yang aneh. Seperti ide jika sesuatu yang ada dikalikan dengan 0 maka menjadi tidak ada. Mungkinkah 5*0 menjadi tidak ada? (* adalah perkalian). Ide ini membuat orang frustrasi. Apakah nol ahli sulap?

Lebih parah lagi-tentu menambah bingung-mengapa 5+0=5 dan 5*0=5 juga? Memang demikian aturannya, karena nol dalam perkalian merupakan bilangan identitas yang sama dengan 1. Jadi 5*0=5*1. Tetapi, benar juga bahwa 5*0=0. Waw. Bagaimana dengan 5^o=1, tetapi 50^o=1 juga? Ya, sudahlah. Aturan lain tentang nol yang juga misterius adalah bahwa suatu bilangan jika dibagi nol tidak didefinisikan. Maksudnya, bilangan berapa pun yang tidak bisa dibagi dengan nol. Komputer yang canggih bagaimana pun akan mati mendadak jika tiba-tiba bertemu dengan pembagi angka nol. Komputer memang diperintahkan berhenti berpikir jika bertemu sang divisor nol.

Bilangan nol: tunawisma

Bilangan disusun berdasarkan hierarki menurut satu garis lurus. Pada titik awal adalah bilangan nol, kemudian bilangan 1, 2, dan seterusnya. Bilangan yang lebih besar di sebelah kanan dan bilangan yang lebih kecil di sebelah kiri. Semakin jauh ke kanan akan semakin besar bilangan itu. Berdasarkan derajat hierarki (dan birokrasi bilangan), seseorang jika berjalan dari titik 0 terus-menerus menuju angka yang lebih besar ke kanan akan sampai pada bilangan yang tidak terhingga. Tetapi, mungkin juga orang itu sampai pada titik 0 kembali. Bukankah dunia ini bulat? Mungkinkah? Bukankah Columbus mengatakan bahwa kalau ia berlayar terus-menerus ia akan sampai kembali ke Eropa?

Lain lagi. Jika seseorang berangkat dari nol, ia tidak mungkin sampai ke bilangan 4 tanpa melewati terlebih dahulu bilangan 1, 2, dan 3. Tetapi, yang lebih aneh adalah pertanyaan mungkinkan seseorang bisa berangkat dari titik nol? Jelas tidak bisa, karena bukankah titik nol sesuatu titik yang tidak ada? Aneh dan sulit dipercaya? Mari kita lihat lebih jauh.

Jika di antara dua bilangan atau antara dua buah titik terdapat sebuah ruas. Setiap bilangan mempunyai sebuah ruas. Jika ruas ini dipotong-potong kemudian titik lingkaran hitam dipindahkan ke tengah-tengah ruas, ternyata bilangan 0 tidak mempunyai ruas. Jadi, bilangan nol berada di awang-awang. Bilangan nol tidak mempunyai tempat tinggal alias tunawisma. Itulah sebabnya, mengapa bilangan nol harus menempel pada bilangan lain, misalnya, pada angka 1 membentuk bilangan 10, 100, 109, 10.403 dan sebagainya. Jadi, seseorang tidak pernah bisa berangkat dari angka nol menuju angka 4. Kita harus berangkat dari angka 1.

Mudah, tetapi salah

Guru meminta Ani menggambarkan sebuah garis geometrik dari persamaan 3x+7y = 25. Ani berpikir bahwa untuk mendapatkan garis itu diperlukan dua buah titik dari ujung ke ujung. Tetapi, setelah berhitung-hitung, ternyata cuma ada satu titik yang dilewati garis itu, yakni titik A(6, 1), untuk x=6 dan y=1. Sehingga Ani tidak bisa membuat garis itu. Sang guru mengingatkan supaya menggunakan bilangan nol. Ya, itulah jalan keluarnya. Pertama, berikan y=0 diperoleh x=(25-0)/3=8 (dibulatkan), merupakan titik pertama, B(8,0). Selanjutnya berikan x=0 diperoleh y=(25-3.0)/7=4 (dibulatkan), merupakan titik kedua C(0,4). Garis BC, adalah garis yang dicari. Namun, betapa kecewanya sang guru, karena garis itu tidak melalui titik A. Jadi, garis BC itu salah.

Ani membela diri bahwa kesalahan itu sangat kecil dan bisa diabaikan. Guru menyatakan bahwa bukan kecil besarnya kesalahan, tetapi manakah yang benar? Bukankah garis BC itu dapat dibuat melalui titik A? Kata guru, gunakan bilangan nol dengan cara yang benar. Bagaimana kita harus membantu Ani membuat garis yang benar itu? Mudah, kata konsultan Matematika. Mula-mula nilai 25 dalam 3x+7y harus diganti dengan hasil perkalian 3 dan 7 sehingga diperoleh 3x+7y=21.

Selanjutnya, dalam persamaan yang baru, berikan y=0 diperoleh x=21/3=7 (tanpa pembulatan) itulah titik pertama P(6,1). Kemudian berikan nilai x=0 diperoleh y=21/7 = 3 (tanpa pembulatan), itulah titik kedua Q(0, 3). Garis PQ adalah garis yang sejajar dengan garis yang dicari, yakni 3x+7y=25. Melalui titik A tarik garis sejajar dengan PQ diperoleh garis P1Q1. Nah, begitulah. Sang murid telah menemukan garis yang benar berkat bantuan bilangan nol.

Akan tetapi, sang guru masih sangat kecewa karena sebenarnya tidak ada satu garis pun yang benar. Bukankah dalam persamaan 3x1+7x2=25 hanya ada satu titik penyelesaian yakni titik A, yang berarti persamaan 3x1+7x2 itu hanya berbentuk sebuah titik? Bahkan pada persamaan 3x1+7x2=21 tidak ada sebuah titik pun yang berada dalam garis PQ. Oleh karena itu, garis PQ dalam sistem bilangan bulat, sebenarnya tidak ada. Aneh, bilangan nol telah menipu kita. Begitulah kenyataannya, sebuah persamaan tidak selalu berbentuk sebuah garis.

Bergerak, tetapi diam

Bilangan tidak hanya terdiri atas bilangan bulat, tetapi juga ada bilangan desimal antara lain dari 0,1; 0,01; 0,001; dan seterusnya sekuat-kuat kita bisa menyebutnya sampai sedemikian kecilnya. Karena sangat kecil tidak bisa lagi disebut atau tidak terhingga dan pada akhirnya dianggap nol saja. Tetapi, ide ini ternyata sempat membingungkan karena jika bilangan tidak terhingga kecilnya dianggap nol maka berarti nol adalah bilangan terkecil? Padahal, nol mewakili sesuatu yang tidak ada? Waw. Begitulah.

Berdasarkan konsep bilangan desimal dan kontinu, maka garis bilangan yang kita pakai ternyata tidak sesederhana itu karena antara dua bilangan selalu ada bilangan ke tiga. Jika seseorang melompat dari bilangan 1 ke bilangan 2, tetapi dengan syarat harus melompati terlebih dahulu ke bilangan desimal yang terdekat, bisakah? Berapakah bilangan desimal terdekat sebelum sampai ke bilangan 2? Bisa saja angka 1/2. Tetapi, anda tidak boleh melompati ke angka 1/2 karena masih ada bilangan yang lebih kecil, yakni 1/4. Seterusnya selalu ada bilangan yang lebih dekat... yakni 0,1 lalu ada 0,01, 0,001, ..., 0,000001. demikian seterusnya, sehingga pada akhirnya bilangan yang paling dekat dengan angka 1 adalah bilangan yang demikian kecilnya sehingga dianggap saja nol. Karena bilangan terdekat adalah nol alias tidak ada, maka Anda tidak pernah bisa melompat ke bilangan 2?

Disadur dari: http://www.duniaesai.com/sains/sains16.htm